Blow-up for Semidiscretizations of some Semilinear Parabolic Equations with a Convection Term

N'Guessan Koffi; Diabate Nabongo; Toure Kidjegbo Augustin

N'Guessan Koffi UFR SED, Alassane Ouattara University of Bouake, 01 BP V 18 Bouake 01 Côte d'Ivoire
Diabate Nabongo UFR SED, Alassane Ouattara University of Bouake, 01 BP V 18 Bouake 01, Côte d'Ivoire
Toure Kidjegbo Augustin Institut National Polytechnique Houphouet-Boigny de Yamoussoukro, BP 1093 Yamoussoukro, Côte d'Ivoire

Keywords: Burgers' equation, semidiscretizations, discretizations, parabolic equations, convection term, blow-up, blow-up time, convergence.

Abstract

This paper concerns the study of the numerical approximation for the following parabolic equations with a convection term

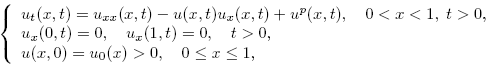
where p > 1.

We obtain some conditions under which the solution of the semidiscrete form of the above problem blows up in a finite time and estimate its semidiscrete blow-up time. We also prove that the semidiscrete blow-up time converges to the real one, when the mesh size goes to zero. Finally, we give some numerical experiments to illustrate ours analysis.

Downloads

Download data is not yet available.

References

Abia L., J. C., Lopez-Marcos J. C. and Martinez J., On the blow-up time convergence of semidiscretizations of reaction-diffusion equations, Appl. Numer. Math., 26 (1998), pp.399-414.

J. Bec, K. Khanin, Burgers turbulence, Physics Reports, 447, (2007), 1-66.

J. von Below, An existence result for semilinear parabolic network equations with dynamical node conditions, Progress in partial Differential equations : elliptic and parabolic problems, Pitman Research Notes in Math. Ser. Longman Harlow Essex, 266, (1992), 274-283.

J. von Below, Parabolic network equations. Tubin0gen, 2 édition, (1994).

J. von Below, C. De Coster, A Qualitative Theory for Parabolic Problems under Dynamical Boundary Conditions, Journal of Inequalities and Applications, 5, (2000), 467-486.

J. von Below, S. Nicaise, Dynamical interface transition in ramified media with diffusion, Comm. Partial Differential Equations, 21, (1996), 255-279.

J. von Below, G. Pincet-Mailly, Blow up for Reaction Diffusion Equations Under Dynamical Boundary Conditions, Communications in Partial Differential Equations, 28, (2003), 223-247.

J. von Below, G. Pincet-Mailly, Blow-up for some nonlinear parabolic problems with convection under dynamical boundary conditions, Discrete and Continuous Dynamical Systems, Supplement Volume,

(2007),10311041.

J. von Below, G. Pincet-Mailly, J-F. Rault, Growth order and blowup points for the parabolic Burgers’ equation under dynamical boundary conditions, Discrete contin. Dyn. Syst. Ser. S., 6(3), (2013), 825-836.

S. Chen, Global existence and blow-up of solutions for a parabolic equation with a gradient term, Proc. Amer. Math. Soc., 129, (2001), 975-981.

M. Chipot, F.B. Weissler Some blow-up results for a nonlinear parabolic equation with a gradient term, SIAM J. Math. Anal., 20, (1989), 886-907.

M. Chlebik, M. Fila, P. Quittner, Blow-up of positive solutions of a semilinear parabolic equation with a gradient term, Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal., 10, (2003), 525-537.

J. Ding, Blow-up solutions for a class of nonlinear parabolic equations with Dirichlet boundary conditions, Nonlinear Anal., 52, (2003), 16451654.

J. Ding, B.-Z. Guo, Global and blow-up solutions for nonlinear Parabolic equations with a gradient term, Houston Journal of Mathematics, 37 (4), (2011), 1265-1277.

J. Ding, B.-Z. Guo, Global existence and blow-up solutions for quasilinear reaction-diffusion equations with a gradient term, Applied Mathematics Letters, 24, (2011), 936-942.

M. Fila, Remarks on blow-up for a nonlinear parabolic equation with a gradient term, Proc. Amer. Math. Soc, 111, (1991), 795-801.

U. Frisch, Turbulence: The legacy of A.N. Kolmogorov, Cambridge University Press, (1995).

O. Ladyzenskaya, V. Solonnikov, N. Uraltseva, Linear and quasilinear equations of parabolic type, Trans. of Math. Monographs, 23, (1968).

G. Pincet-Mailly, J-F. Rault, Nonlinear convection in reaction-diffusion equations under dynamical boundary

conditions, Electronic Journal of Differential Equations, 2013(10), (2013), 1-14.

J-F. Rault, Phénomène d’explosion et existence globale pour quelques problèmes paraboliques sous les conditions au bord dynamiques, PhD thesis, Université du Littoral Côte d’Opale, (2010).

J-F. Rault, A Bifurcation for a Generalized Burgers’ Equation in Dimension One, Discrete contin. Dyn. Syst. Ser. S., 5(3), (2012),683-706.

P. Souplet, Finite time blow-up for a non-linear parabolic equation with a gradient term and applications, Math. Methods Appl. Sci., 19, (1996), 1317-1333.

P. Souplet, Recent results and open problems on parabolic equations with gradient nonlinearities, Electronic Journal of Differential Equations, 2001(20),(2001), 1-19.

P. Souplet, F. Weissler, Self-Similar Subsolutions and Blow-up for Nonlinear Parabolic equations, Journal of

Mathematical Analysis and Applications, 212, (1997), 60-74.

P. Souplet, S. Tayachi, F. B. Weissler, Exact self-similar blow-up of solutions of a semilinear parabolic equation with a nonlinear gradient term, Indiana Univ. Math. J., 45, (1996), 655-682.

M. M. Taha, A. K. Touré and P. E. Mensah, Numerical approximation of the blow-up time for a semilinear parabolic equation with nonlinear boundary conditions, Far East journal of Mathematical Sciences (FJMS), 60(45), (2012), 125-167.

F. Weissler, Existence and nonexistence of global solutions for a semilinear heat equation. Israel Journal of Mathematics, 38, (1981), 29-40.