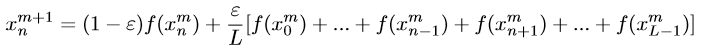On the globally coupled lattice system (GCM) associated with the Belusov-Zhabotinskii reaction (p,q)-points on the coupling constant ε ∈ (0,1]

Xin Chen; Kai Yu; Yuhan Kang; Chunlu Wangxia

Xin Chen Department of Applied Mathematics, Sichuan Agricultural University, Ya’an, Sichuan, 625014, P.R. China
Kai Yu Department of Applied Mathematics, Sichuan Agricultural University, Ya’an, Sichuan, 625014, P.R. China
Yuhan Kang Department of Applied Mathematics, Sichuan Agricultural University, Ya’an, Sichuan, 625014, P.R. China
Chunlu Wangxia Department of Applied Mathematics, Sichuan Agricultural University, Ya’an, Sichuan, 625014, P.R. China

Keywords: Globally coupled system; distributionally (p, q)-chaos; Measure

Abstract

This paper focuses on the Global Coupling System (GCM) associated with the Belusov-Zhabotinskii reaction:
捕获.PNG

where m is discrete time index, n is lattice side index with system size L, ε ∈ (0,1] is coupling constant and f_n is a continuous selfmap on [0,1] for every n ∈ {1,2,··· ,L}.We prove that the system is distributionally (p,q)-chaotic on the non-zero coupling constant ε ∈ (0,1), and its main metric is not less than 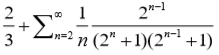捕获1.PNG 。

Downloads

Download data is not yet available.

References

[1] T.Y. Li, J.A. Yorke, Period three implies chaos. Am. Math. Mon. 82(10), 985-992 (1975)
[2] L.S. Block, W.A. Coppel, Dynamics in One Dimension, Springer Monographs in Mathematics(Springer, Berlin, 1992)
[3] Kaneko K.Theory and Application of Coupled Map Lattices.Ann Arbor: John Wiley and Sons,1983.
[4] R. Bowen, Entropy for group endomorphisms and homogeneous spaces. Trans. Am. Math. Soc. 153, 401-414 (1971)
[5] B. Schweizer, J. Smfftal, Measures of chaos and a spectral decomposition of dynamical systems on the interval. Trans. Am. Math. Soc. 344, 737-754 (1994)
[6] D.L. Yuan, J.C. Xiong, Densities of trajectory approximation time sets (in Chinese). Sci. Sin. Math. 40(11), 1097-1114 (2010) (2010). B. Schweizer, A. Sklar, J. Smfftal, Distributional
(and other) chaos and its measurement. Real Anal.189 Exch. 21, 495-524 (2001)
[7] J.L. Garcffa Guirao, M. Lampart, Positive entropy of a coupled lattice system related with Belusov?Zhabotinskii reaction. J. Math. Chem. 48, 66-71 (2010)
[8] X.X. Wu, P.Y. Zhu, The principal measure and distributional (p,q)-chaos of a coupled lattice system related with Belusov-Zhabotinskii reaction. J. Math. Chem. 50, 2439-2445 (2012)
[9] J.L. Garcffa Guirao, M. Lampart, Chaos of a coupled lattice system related with BelusovZhabotinskii reaction. J. Math. Chem. 48, 159-164 (2010)
[10] J.L. Garcffa Guirao, M. Lampart, Positive entropy of a coupled lattice system related with Belusov–Zhabotinskii reaction. J. Math. Chem. 48, 66-71 (2010)
[11] X.X. Wu, P.Y. Zhu, The principal measure and distributional (p,q)-chaos of a coupled lattice system related with Belusov-Zhabotinskii reaction. J. Math. Chem. 50, 2439-2445
(2012)